Spontaneous symmetry breaking (SSB) is one of the most fundamental concepts of nonlinear science that has been studied in many fields, ranging from condensed-matter physics to high-energy physics, and from Bose–Einstein condensates to nonlinear optical physics. The SSB of solitons has intrigued many physicists in recent years.
However, the influence of SSB on different kinds of solitons is just surveyed in conventional nonlinear physical, causing the undiscover of underlying physical mechanism in purely nonlinear fractional quantum mechanics with space fractional derivatives.
Previously researches have presented that different linear and nonlinear properties of the propagation of light in space-fractional quantum mechanics, described by linear and nonlinear fractional Schrödinger equations. Yet, the underlying mechanism remains missing. Are there any methods to deeply explain this phenomenon?
A research team led by Prof. Dr. ZENG jianhua from Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) firstly proposed an in-depth insight of the SSB phenomenon thereof. The results were published in Chaos.
In their model, both 1D symmetric, asymmetric, and anti-symmetric soliton states, pinned in the nonlinear double-well pseudopotential, are demonstrated; linear and dynamic stabilities of these states are both taken into account, performed numerically based on a computation of stability eigenvalues and direct perturbed simulations.
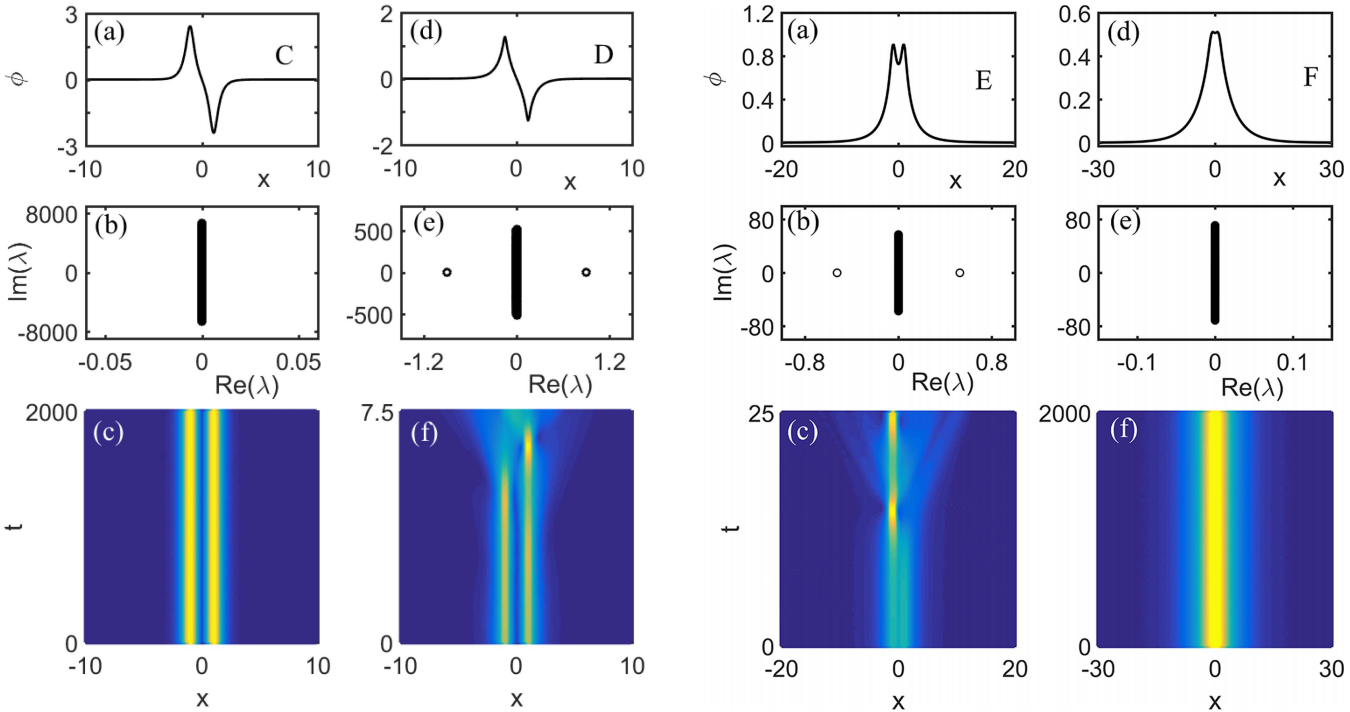Numerical results calculated from presented model (Image by XIOPM)
With a finding of symmetry-breaking bifurcation points at which the SSB bifurcation occurs, while below the bifurcation both the symmetric and anti-symmetric solutions are stable.
Moreover, the existence and stability of all the soliton states are obtained with the combined usages of linear-stability analysis and direct perturbed simulations.
The presented model shed new light on promising experiments in the contexts of nonlinear optics and Bose–Einstein condensates. As a promotion or a new development, it is natural to extend the presented results to higher dimensional systems.
Download：