Solitons, nonlinear particle-like excitations with inalterable properties (amplitude, shape, and velocity) as they propagate, are omnipresent in many branches of science-and in physics in particular. Flat-top solitons are a novel type of bright solitons that have not been well explored in pure nonlinear media. Here, a model of nonlinear Kerr (cubic) media of ultracold atoms with spatially modulated repulsive interactions is proposed and shown by Jianhua Zeng’s research team to support a vast variety of stable flat-top matter-wave solitons, including one-dimensional flat-top fundamental and multipole solitons, and two-dimensional flat-top fundamental and vortex solitons. They demonstrate that by varying the relevant physical parameters (nonlinearity coefficient and chemical potential), the ordinary bright (Gaussian) solitons can transform into the novel flat-top solitons. The (in)stability domains of the flat-top soliton families are checked by means of linear stability analysis and reconfirmed by direct numerical simulations. This model is generic in the contexts of nonlinear optics and Bose-Einstein condensates, which provides direct experimental access to observe the predicted solutions.
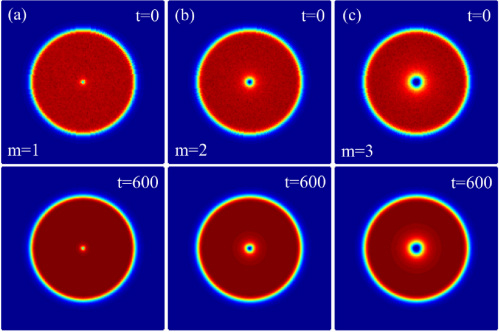
(Original research article "Journal of the Optical Society of America B Vol.36, Issue 8, pp. 2278-2284 (2019) https://www.osapublishing.org/josab/abstract.cfm?uri=josab-36-8-2278")
Download: