We present a novel and straightforward Fibonacci lens, which is created by binarizing and adding a spiral phase to its radial phase function. It is shown that this new element yields a pair of petal-like modes due to several segments of the Fibonacci lens, where each segment is phase shifted by $\pi$ compared to its adjacent segment. Also, the generated petals have highly controllable rotation, and their locations are adjustable, in which their focal distance ratio is equal to a mathematical parameter of the so-called golden ratio. Also, by changing the topological charge, an arbitrary even number of petals is obtained.
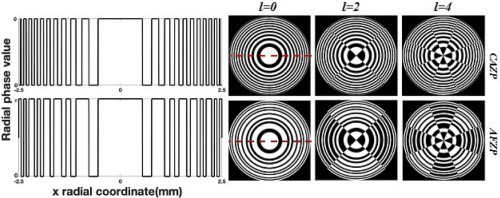
CAZP and AFZP with the same zones of $N = 21$ are shown in the first and second rows, respectively.
Download: