Spontaneous symmetry breaking, a spontaneous course of breaking the spatial symmetry (parity) of the system, is known to exist in many branches of physics, including condensed-matter physics, high-energy physics, nonlinear optics, and Bose–Einstein condensates. In recent years, the spontaneous symmetry breaking of solitons in nonlinear wave systems is broadly studied; understanding such a phenomenon in nonlinear fractional quantum mechanics with space fractional derivatives (the purely nonlinear fractional systems whose fundamental properties are governed by a nonlinear fractional Schr？dinger equation), however, remains pending. Here, we survey symmetry breaking of solitons in fractional systems (with the fractional diffraction order being formulated by the Lévy index α) of a nonlinear double-well structure and find several kinds of soliton families in the forms of symmetric and anti-symmetric soliton states as well as asymmetric states. Linear stability and dynamical properties of these soliton states are explored relying on linear-stability analysis and direct perturbed simulations, with which the existence and stability regions of all the soliton families in the respective physical parameter space are identified.
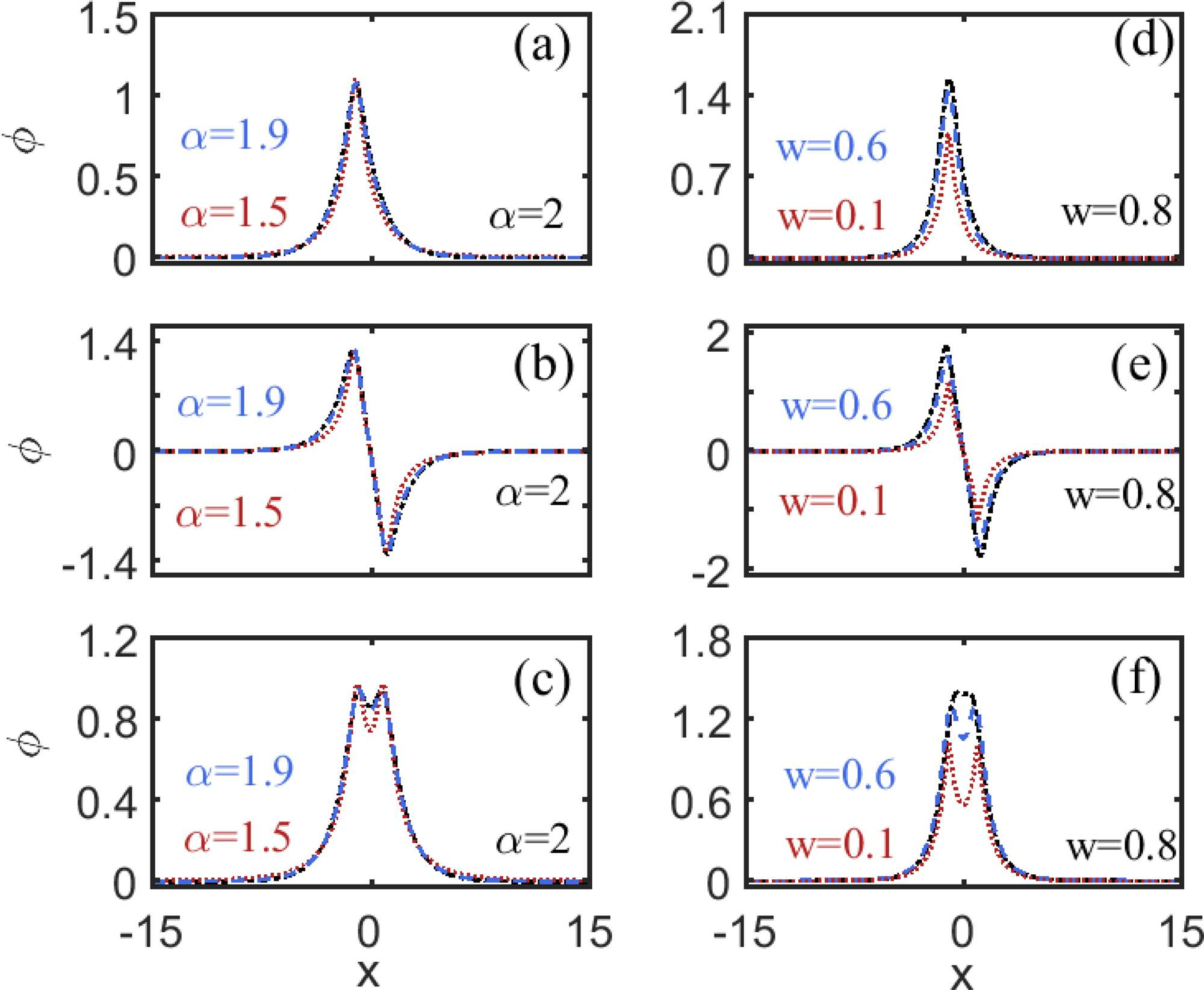Profiles of (a) asymmetric, (b) anti-symmetric, and (c) symmetric soliton states with w = 0.5, b = 0.3, and different values of α. Profiles of (d) asymmetric, (e) anti-symmetric, and (f) symmetric soliton states with α = 1.8, b = 0.6, and different values of w. (Image by XIOPM)
Download：