From advanced mathematics, we can know that integral calculus is a general formal theory of integral and derivative of integer order. The "fractional integral", was firstly proposed in mathematics half a century ago, it was a theory about fractional integral and derivatives.

With the development of theoretical physics, the systems of fractional calculus are now progressing to describe the actual physical situations including quantum mechanics, optics, ultracold atomic gases, and condensed matter.

In classical quantum mechanics, the basic equation describing particle diffusion is described by Feynman path integral theory based on Brownian motion. However, for non-Brownian motion paths, the corresponding eigen equation becomes the diffusion equation of fractional integrals.

Therefore, how to explain the existence and stability of various localized modes in nonlinear fractional systems is still a huge challenge.

A research team led by Prof. Dr. ZENG Jianhua from Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) made a remarkable progress in this field and they successfully explained the existence and stability of various localized modes in nonlinear fractional systems. The results were published in ADVANCED THEORY AND SIMULATIONS.

According to the researchers, there are normally two approaches to describe the nonlinear wave mechanics equations in periodic structures: coupled mode equations and discrete nonlinear Schr?dinger equations. However, both of these methods have limitations: the former can only describe the shallow lattice, while the latter can only describe the deep lattice and is only applicable to the local case of nonlinear waves.

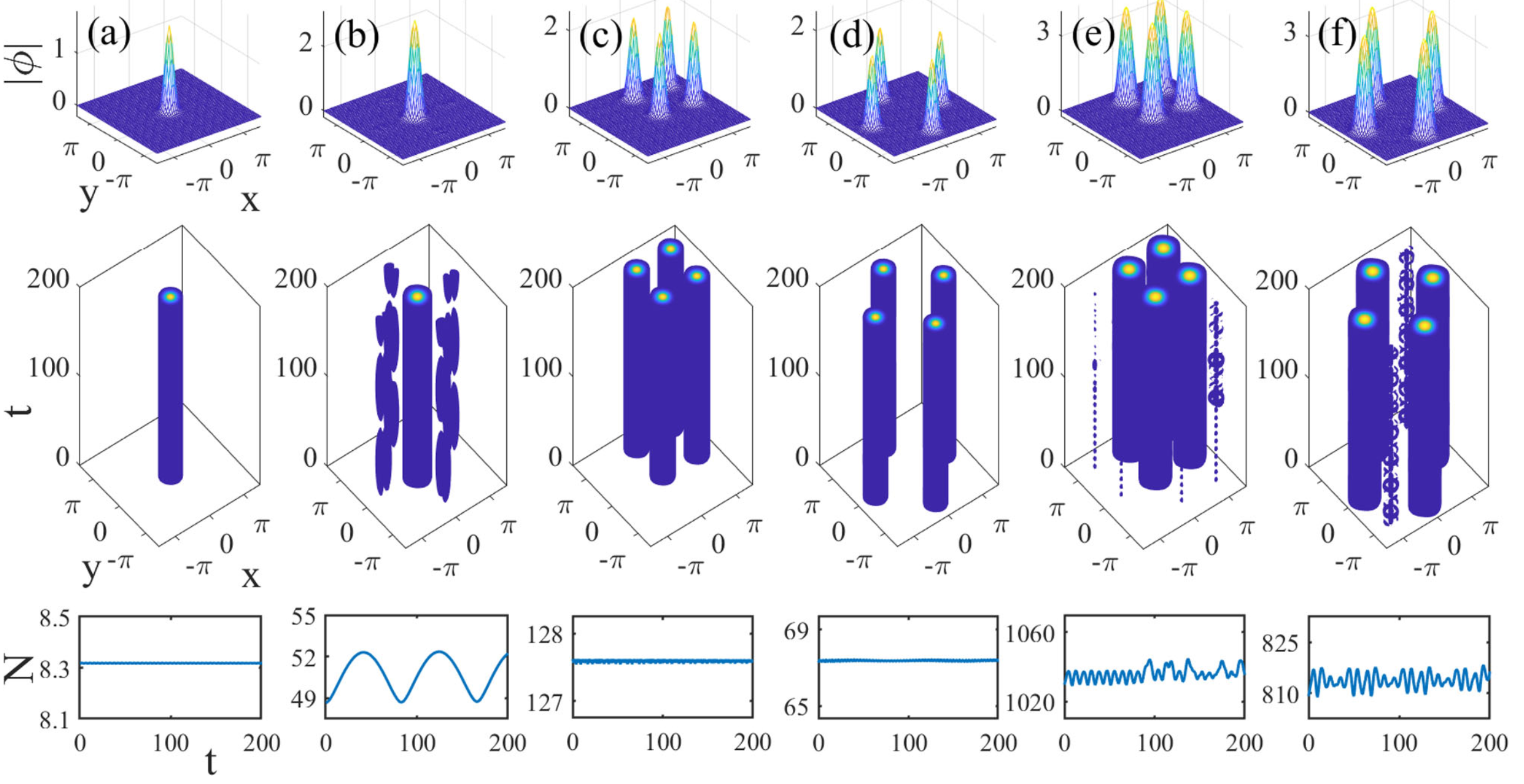
Therefore, they began from the continuity equation under the mean-field approximation, and deeply investigated the ultracold atomic lattice including its generation, features, and stability of the nonlinear localized modes. Moreover, they mainly focused on the defocusing of third order nonlinear (corresponding to the Kerr effect in optics) gap is located in the first region and a second band gap under the action of physical properties and the band gap of the vortex band gap soliton.

Finally, the existence, structure, and dynamics of 1D and 2D gap solitons (GSs) were detailly analyzed. The 1D GSs are strongly confined in a single lattice cell, as well as the 2D GSs and vortices found here are unstable only very close to edges of the bandgaps.

The remarkable performances make the proposed approach feasible application because it can be realized by the current conditions of physical systems.

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11704066, 12074423, 12074063), and the Jiangxi Provincial Natural Science Foundation (Grant No. 20202BABL211013)

The contour shapes of the electromagnetically induced moiré optical lattice potentials. (Image by XIOPM)