Dark solitons, which are characterized as localized intensity dips below a continuous wave background, have attracted great attention due to its fascinating property.

At present, the mainstream researches focus on ultracold atoms like Bose-Einstein condensates (BECs) which have been confirmed to be able to stably generate optical solitons. BECs also exhibit different dimensionality and configurations, and provide a clear research platform. However, when it comes to multidimensional BECs, the dark solitons tend to become instable which mainly initiated by transverse modulational instability.
Now a research team led by Prof. Dr. ZENG Jianhua from the Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) has proposed a purely nonlinear strategy to stabilize dark-soliton stripes. Their results were published in Chaos, Solitons & Fractals.

The researchers anatomized the existence, property and dynamics of dark-soliton stripe modes in two-dimensional BECs. With the Gross-Pitaveski/nonlinear Schr?dinger equation derived from the Maxwell-Bloch equations, they got the steady-state dark soliton stripe modes through the variational approximation and linear-stability analysis，and introduced quasi-one-dimensional Gaussian like trap and its combination with the external linear harmonic trap to realize the stabilization mechanism of dark-soliton stripes.

Direct numerical simulations matched well with the theoretical ways above and revealed that the snaking-instability wave number band could be shortened by the purely nonlinear trap, making the dark soliton stripe stable. Further, the research team demonstrated the formation of stable dark-soliton stripes in the combined focusing nonlinear trap and linear harmonic trap, breaking the stereotype that the dark solitons could only exist in repulsive (defocusing) Kerr nonlinearity. Particularly, the defocusing nonlinear trap under the action of linear harmonic trap could also help to stabilize dark-soliton stripes against the underlying snaking instability.

Although the present work remains still in the stage of theory and simulation, researchers believed that this predicted result may be realized in Bose-Einstein condensates and nonlinear optics.

This work was supported by the National Natural Science Foundation of China (NSFC).

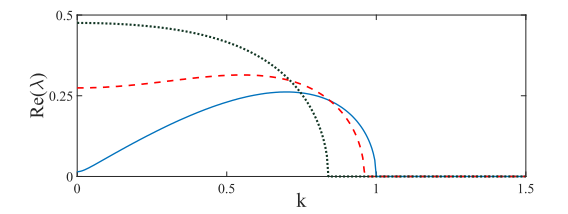
The growth rate, expressed as maximal real part of eigenvalues Re(λ) of the transverse modulational instability of dark-soliton stripes under different values of the height (g0) and width (σ) of the nonlinear trap, in the absence of external linear harmonic trap. (Image by XIOPM)

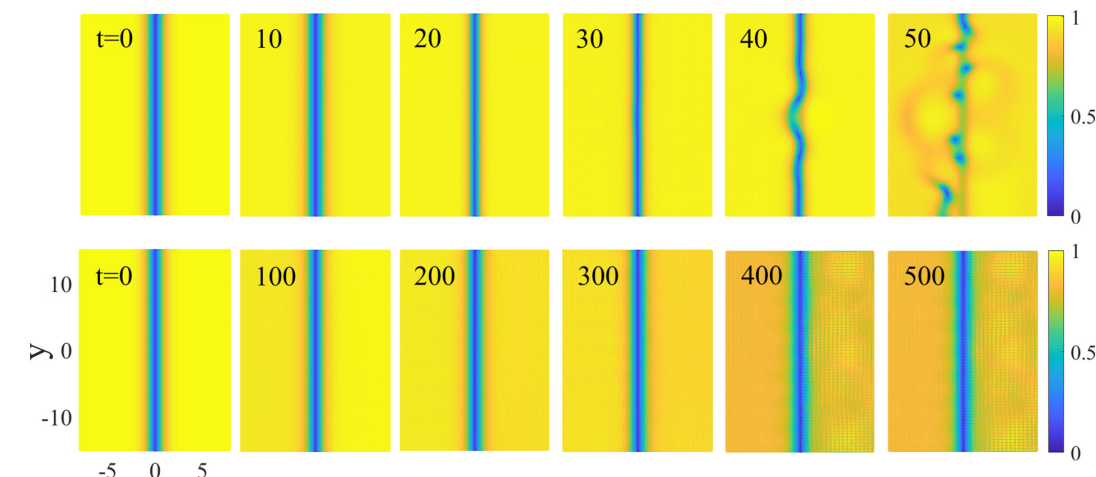
The dynamical evolution of dark-soliton stripes created in a nonlinear trap under the action of transverse modulational instability and without taking the external linear harmonic trap. (Image by XIOPM)

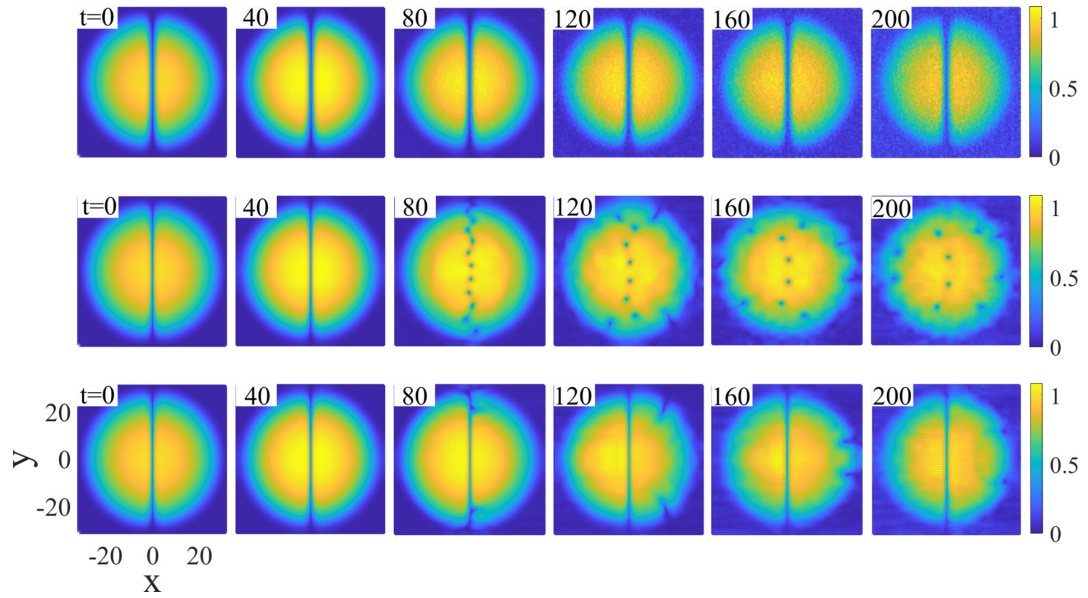
Dynamics of dark-soliton stripes affected by the associated transverse modulational instability in the BEC with localized nonlinear distribution and loaded onto an external harmonic trap having a strength ω = 0.05. (Image by XIOPM)