The acceleration of computation is of great interests in the recent years, due to the rapidly development of practical applications including finance, machine learning and circuit design. Those applications can hardly be solved by using normal personal computers, which requires the novel technology to achieve mass computation.

A research team led by Dr. LIU Hongjun from Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) proposed a novel design to achieve the accuracy-enhanced coherent Ising machine (CIM) by using the quantum adiabatic theorem. The results were published in OPTICS EXPRESS.

Traditional approaches to accelerate computational inevitably have large size, which severely restrict their further applications. The CIM based on optical parametric oscillator network has been proven to be the most promising method recently, because the CIM can take the advantages of high speed and parallelization of the light.

The researchers were inspired by a novel physical system, which is time-multiplexed degenerate optical parametric oscillators (DOPOs) and measurement-feedback approach. The DOPO pulses can represent an Ising spin and the in-phase amplitude, which can enhance the performance of CIM.

Firstly, the continuous time-dependent Ising Hamiltonian was calculated to investigate the adiabatic evolution on networks of DOPOs. Therefore, by randomly flipping a few spins at the end of each adiabatic step to decrease the Ising energy, the machine can continue evolving towards the Ising ground state.

Moreover, the machine performance depends on the annealing time was also investigated. The results indicate that the time-dependent Hamiltonian during at least 20 evolution steps to ensure the effectiveness of the adiabatic evolution.

To see how the performance of the proposed CIM scales to larger problem size, the researchers solved the sparsely connected G-set instances and fully connected complete graphs with the number of vertices ranging from 800 to 2000. The outcomes show the performance improvement of the proposed CIM with respect to the CIM. The computational accuracy of the proposed CIM is increased from 0.124% to 0.754% compared with the CIM.

The proposed CIM has the potential research direction, which can be extended to solve more complex Ising Hamiltonian and physical models.

This work was supported by the National Natural Science Foundation of China.

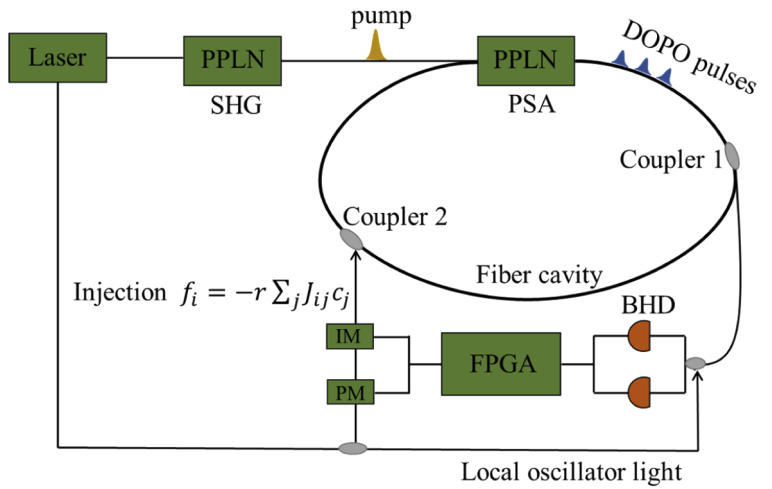
The schematic of the CIM with measurement-feedback control. (Image by XIOPM)