Nonlinear Fractional Schr？dinger Equation (NLFSE) is the fundamental equation in nonlinear regimes, such as self‐focusing or self‐defocusing cubic (Kerr) nonlinearity and saturable nonlinearity with either cubic or quintic terms. It is a hallmark physical model of light propagation in nonlinear optical media, which is also adopted in soliton properties investigation recently.

However, the propagation of laser beams in nonlinear saturable media with fractional diffraction has not been elaborately surveyed in great detail. The formation and propagation stability of solitons in 1D saturable fractional media with nonlinear lattice schemes are unclear.

To set up a physical model under the nonlinear fractional Schr？dinger equation with spatial fractional derivative and saturable nonlinearity is an urgent work in soliton research field.

A research team led by Prof. Dr. ZENG Jianhua from Xi'an Institute of Optics and Precision Mechanics (XIOPM) of the Chinese Academy of Sciences (CAS) carried out a general theoretical analysis of light-wave propagation in space-fractional media based on NLFSE model. The stable dipole solitons within a single well of the nonlinear lattice was presented.The result was published in ANN PHYS-BERLIN. (https://doi.org/10.1002/andp.201900385).

The model upholds two kinds of one dimensional soliton families, including fundamental solitons (single peak) and higher-order solitonic structures consisting of two-hump solitons (in-phase) and dipole ones (anti-phase).

Such new model permits the existence of two classes of 1D soliton families, that is, fundamental solitons (with single hump) and the higher-order nonlinear excitations consisting of two-hump solitons (in-phase) and dipole modes (anti-phase). 

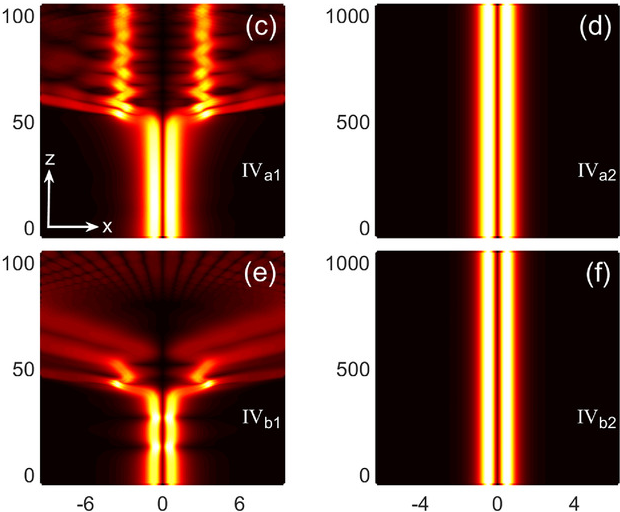       Dipole (anti‐phase) solitons localized in a single well of the nonlinear lattice. (Image by XIOPM)

Notably, the dipole solitons can be robust stable physical objects localized merely within a single well of the nonlinear lattices—previously thought impossible.

Such single-well localized dipole modes represent a new fundamental class of dipole solitons in the purely nonlinear periodic systems without any (linear) external potentials--previous results of dipole solitons in the general quantum mechanics framework were only restricted to the double-well localized modes.

Thus, its discovery supplements and completes the dipole soliton families in the purely nonlinear media.

These results signify that the fractional diffraction control in the space-fractional physical systems provides another flexible and important freedom for steering the light-wave or matter-wave dynamics, which can be experimentally realized in optics and beyond.