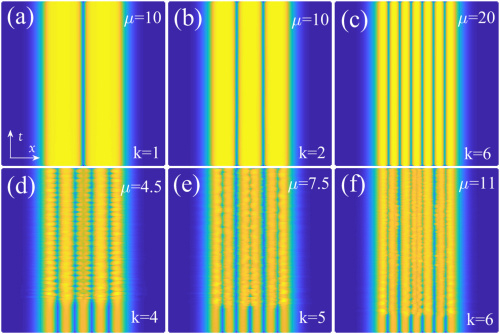
Jianhua Zeng’s research team elaborated one- and two-dimensional (1D and 2D) models of media with self-repulsive cubic nonlinearity, whose local strength is subject to spatial modulation that admits the existence of flat-top solitons of various types, including fundamental ones, 1D multipoles, and 2D vortices. Previously, solitons of this type were only produced by models with competing nonlinearities. The present setting may be implemented in optics and Bose-Einstein condensates. The 1D version gives rise to an exact analytical solution for stable flat-top solitons, and generic families may be predicted by means of the Thomas-Fermi approximation. Stability of the obtained flat-top solitons is analyzed by means of the linear-stability analysis and direct simulations. Fundamental solitons and 1D multipoles with k=1 and 2 nodes, as well as vortices with winding number m=1, are completely stable. For multipoles with k >= 3 and vortices with m >= 2, alternating stripes of stability and instability are identified in their parameter spaces.

（Original research article "Optics Letters Vol. 44, Issue 5, pp. 1206-1209 (2019) https://www.osapublishing.org/ol/fulltext.cfm?uri=ol-44-5-1206&id=406014"）