Recently, optical vortices (OVs) have attracted substantial attention because they can provide an additional degree of freedom, i.e., orbital angular momentum (OAM). It is well known that the fractional OV (FOV) is interpreted as a weighted superposition of a series of integer OVs containing different OAM states. However, methods for controlling the sampling interval of the OAM state decomposition and determining the selected sampling OAM state are lacking. To address this issue, in this Letter, we propose a FOV by inserting multiple fractional phase jumps into whole phase jumps (2π), termed as a multi-fractional OV (MFOV). The MFOV is a generalized FOV possessing three adjustable parameters, including the number of azimuthal phase periods (APPs), N; the number of whole phase jumps in an APP, K; and the fractional phase jump, α. The results show that the intensity and OAM of the MFOV are shaped into different polygons based on the APP number. Through OAM state decomposition and OAM entropy techniques, we find that the MFOV is constructed by sparse sampling of the OAM states, with the sampling interval equal to N. Moreover, the probability of each sampling state is determined by the parameter α, and the state order of the maximal probability is controlled by the parameter K, as K * N. This work presents a clear physical interpretation of the FOV, which deepens our understanding of the FOV and facilitates potential applications, especially for multiplexing technology in optical communication based on OAM.

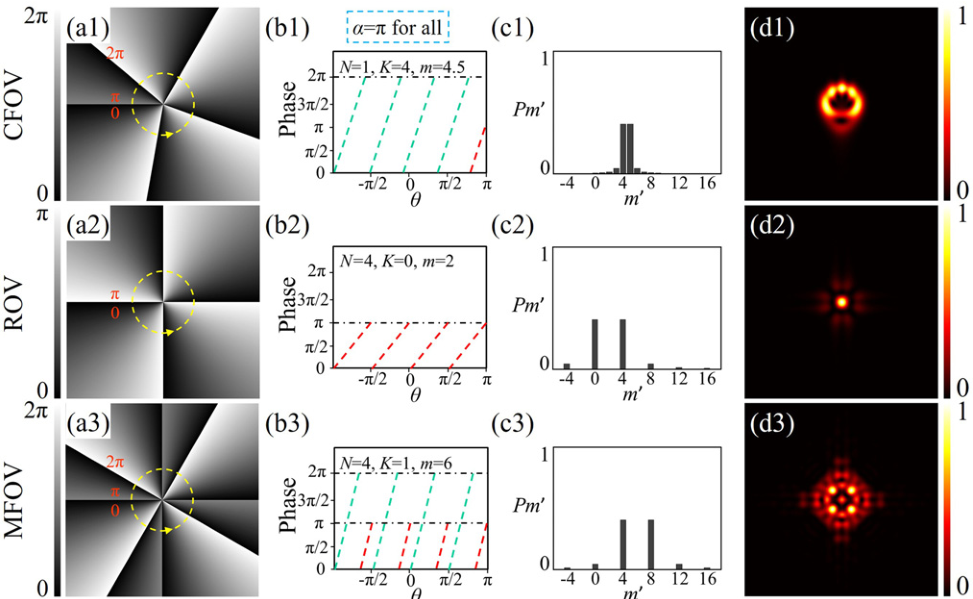
Schematic for the generation of the CFOV, ROV, and MFOV. (Image by XIOPM)